Affichage des résultats 1 à 30 sur 30
Discussion: Influence de la focale en portrait
Vue hybride
-
12/08/2012, 02h39 #1Membre

- Inscription
- mars 2012
- Localisation
- Siebnen, Zurich, Suisse
- Âge
- 44
- Messages
- 318
- Boîtier
- 6D, 7DII
- Objectif(s)
- Canon 35/2, 50/1.8, 85/1.8, Canon16-35/2.8, Tamron 70-200/2.8IS, Canon 24-70/2.8

Alors, pour mettre un peu de math la dedans.
Tout est question de rapport de distances.
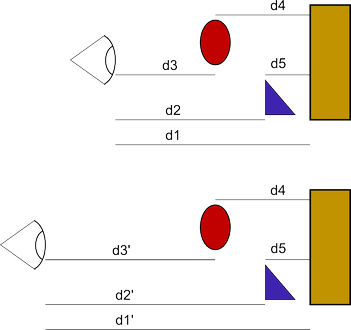
Regardons ma magnifique illustration.
Les distances d1 et d1' représentent la distance de l'œil (ou de la
camera) a l'objet du fond (mettons le mur de la pièce). Les distances
d2,d3,d2',d3' sont celles des objets a l'observateur. Toutes ces distances
varient en fonction de la position de l'observateur. En revanche, les
distances d4 et d5 restent fixes, quelque soit la position de
l'observateur.
On suppose donc que d1<d1', d2<d2' et d3 < d3'.
Quid des rapports : d4/d1', d5/d1', d3'<d1' et d4'/d1' :
Si on suppose que d1' tend vers l'infini (on est donc loin) alors les
rapports tendent tous vers 0. Resultat, impossible de distinguer si le
rond est plus proche ou plus loin que le triangle et on a l'impression
qu'ils sont dans le mur.
En revanche, si on a d3 qui tend vers 0 (donc très proche du rond) et en
supposant que l'on puisse quand même voir les objets derrière le rond.
Nous avons donc les rapport d4/d3, d5/d3 qui tendent vers l'infini. On a
donc l'impression que le triangle et le mur se trouvent très très loin.
Ce qui montre bien que c'est la distance entre l'observateur et les objets
qui définie les perspectives.
Informations de la discussion
Utilisateur(s) sur cette discussion
Il y a actuellement 1 utilisateur(s) naviguant sur cette discussion. (0 utilisateur(s) et 1 invité(s))
Discussions similaires
-
Quelle focale fixe portrait/Macro ?
Par Damze dans le forum Discussions ObjectifsRéponses: 21Dernier message: 26/02/2011, 13h17 -
mon budjet a augmenté pour une focale fixe portrait
Par tipiake dans le forum Discussions ObjectifsRéponses: 16Dernier message: 11/08/2010, 11h53 -
Quel objectif focale fixe pour portrait sur aps-c
Par blackdragoon dans le forum Discussions ObjectifsRéponses: 28Dernier message: 24/07/2010, 17h02 -
choix Focale Fixe pour portrait sur APS-C
Par Diogene95 dans le forum Discussions ObjectifsRéponses: 8Dernier message: 12/04/2010, 18h53 -
Flash ou focale fixe 1.4 pour portrait ( budget 250 à 350 euros )
Par ericounet963 dans le forum Discussions FlashRéponses: 19Dernier message: 01/02/2010, 14h05