Affichage des résultats 1 à 10 sur 10
-
29/07/2009, 14h23 #1Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 [AIDE] Tutoriels: netteté, autofocus, micro-réglages, DPI, hyperfocale...
[AIDE] Tutoriels: netteté, autofocus, micro-réglages, DPI, hyperfocale...
Beaucoup de débutants demandent aux membres plus expérimentés du forum de l'aide technique sur un cliché précis. Beaucoup postent en guise d'illustration une photo souvent trop petite et surtout sans les paramètres de prise de vue (appelés EXIFs). Ces paramètres sont naturellement présents dans les fichiers (RAW ou JPG) enregistrés sur la carte mémoire de votre appareil.
Aussi, nous vous demandons pour faciliter la qualité et la rapidité des réponses à vos questions, de donner dans le post :
- Les conditions de prises de vue ("il y avait du vent", "je tenais l'appareil à bout de bras", etc...)
- Éventuellement, pour avoir une première approche visuelle, une version réduite de la photo en affichage direct (selon les limites en vigueur dans le règlement du forum)
- Les fameux EXIFs et notamment : objectif et boitier utilisés, focale utilisée, le trio vitesse/diaphragme/sensibilité
Et, très important :
- Un lien vers le fichier JPG non retouché non redimensionné de la photo (fichier JPG brut, sorti de la carte mémoire)
Ou pour ceux travaillant en RAW :
- Un lien vers le JPG issu directement de la conversion du RAW par Digital Photo Professional (le logiciel fourni gratuitement avec tous les reflex Canon) afin de conserver le plus de métadonnées possibles (comme par exemple, quel collimateur a été utilisé), métadonnées souvent effacées en totalité ou en partie lors de la conversion par des dérawtiseurs tiers.
- Ou un lien vers le fichier RAW lui-même afin de fournir un fichier brut sans post-traitement.
Vous pouvez utiliser ce service de téléchargement comme http://www.1fichier.com et poster dans la discussion le lien (qui commence par http://) qui nous permet de télécharger le fichier. Ce lien est donné par le site après téléchargement, les photos ne sont pas visibles à l'écran (on peut d'ailleurs héberger n'importe quel fichier avec ce service). Si vous avez plusieurs photos à proposer, faites un ZIP et postez ce ZIP sur le site de téléchargement (télécharger plusieurs fichiers prend plus de temps, et souvent les hebergeurs limitent les téléchargements simultanés). Surtout pas d'affichage direct !!! N'utilisez pas les balises [IMG] ou la boite de dialogue Insérer une image. Le post sera supprimé dans le cas contraire.
A+ sur le forum
-
01/08/2009, 11h55 #2Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 Problème d'autofocus ou de netteté
Problème d'autofocus ou de netteté
Nous sommes souvent confrontés dans le forum technique à des problèmes d'autofocus ou de netteté, qui sont dus à un mauvais paramétrage du boitier et/ou l'utilisation d'un mode inadapté. Ces erreurs sont liées à une mauvaise connaissance du matériel, à une transition rapide entre compact tout automatique et reflex, et il faut bien le dire, à une mauvaise (ou une absence de) lecture du manuel livré avec.
D'ailleurs, le texte qui suit contient à 95% des infos qui sont déjà dans le manuel. Je n'ai rien inventé, moi même ayant expérimenté telle ou telle déconvenue quand j'ai commencé à utiliser un EOS (il y a 20 ans de ça), mais sans pour autant remettre en cause immédiatement mon matériel. Un petit tour dans le manuel, et le problème était (souvent) résolu. En photo, c'est bien souvent le photographe le maillon faible, à tout point de vue
Préalable :
- Ca peut paraître bête mais assurez-vous que le commutateur de l'objectif est bien sur AF, sinon évidemment, l'autofocus ne fonctionne pas (mise au point manuelle).
- MAP = Mise Au Point. AF = AutoFocus. PMC = Pression à Mi-Course du déclencheur. Shoot = Pression à fond du déclencheur. PDC = Profondeur De Champ
Vous trouverez donc dans ce topic, diverses situations rencontrées très souvent par les débutants (et les moins débutants !) et qui s'expliquent autrement que par une panne matérielle. Evidemment, loin de moi l'idée de minimiser les vrais problèmes ! Il y en a, le SAV étant dans ce cas un passage obligé. Simplement, à la lecture du forum et des nombreux posts angoissés de leurs auteurs, je trouve dommage de s'imaginer devoir rendre son appareil tout neuf acheté la semaine d'avant alors que le phénomène est normal (et au passage, égratigner Canon, qui n'y est pour rien !). Combien d'appareils sont envoyés au SAV et repartent comme ils sont venus avec une simple note du technicien ?
Si toutefois vous souhaitez confirmation de l'éventuel problème en postant une photo, et pour toute aide technique en général, merci de suivre mes conseils ici afin de savoir ce dont on a besoin pour vous aider. J'insiste sur le fait qu'on ne peut faire aucun diagnostic de netteté ou de piqué si vous ne postez qu'une version réduite.
En effet, on peut avoir ça à 100% (j'ai appliqué un flou gaussien sur mon image pour dégrader le piqué).

Et obtenir une version réduite (certes traitée dans ce but) comme suit :

On voit très bien que la réduction suivie d'une accentuation (voir tuto ici) masque totalement le problème de netteté de la photo d'origine. Donc, SVP, suivez les conseils énoncés dans ce post, afin de pouvoir vous aider efficacement.
Pour commencer, une interrogation un peu différente de celles qui suivent, mais le problème est souvent constaté :
"Quand je réduis mes photos pour les afficher sur le forum, elles sont moins nettes."
C'est normal. Le processus de réduction des images altère une partie de l'image et réarrange les pixels. S'en suit une certaine mollesse qu'il est facile de rattraper ensuite en accentuant un peu l'image déjà réduite. Il est fort probable que le logiciel que vous utilisez pour réduire les photos puisse aussi les accentuer un peu. Pour les réglages, tout est question de dosage. Faites des essais !
Un tuto est consacré à la préparation des images pour l'affichage sur le web. Vous le trouverez ici.
Maintenant, place aux questions réponses sur l'autofocus et la netteté de vos clichés.
1. "Dans mon viseur, rien n'est net, malgré le bip de confirmation de l'AF. Sur l'écran arrière ou sur l'écran de l'ordinateur, pourtant, mes photos sont nettes."
Le réglage dioptrique est mal réglé. Retirez l'objectif, regardez dans le viseur, tournez la molette du réglage dioptrique afin que les collimateurs autofocus soient nets.
2. "Ce n'est pas net à l'endroit où j'ai visé, malgré le bip de confirmation de l'AF. Je trouve pourtant une zone nette dans ma photo."
Vous avez sélectionné un autre collimateur parmi ceux à votre disposition, ou pire, tous les collimateurs sont activés et c'est donc le boitier qui choisit où la MAP doit se faire. Il faut donc en sélectionner un (en général, celui du centre), et viser avec ce collimateur l'endroit où on veut faire la MAP. PMC, bip et lumière de confirmation AF sur le collimateur choisi, shoot.
3a. "Rien n'est net et je n'ai plus le bip et la lumière de confirmation AF."
3b. "Ce n'est pas net à l'endroit où j'ai visé et je n'ai plus le bip et la lumière de confirmation AF."
3c. "Mon autofocus ne s'arrête jamais de fonctionner dès que je fais une PMC et je n'ai plus le bip et la lumière de confirmation AF."
Vous êtes en mode autofocus AI Servo. Ce mode, dédié essentiellement au sport, procure un autofocus continu, qui cherche en permanence à faire le point (utile sur des sujets mobiles), et sans confirmation AF (ni lumière, ni bip), puisque la MAP n'est jamais figée. Sélectionnez le mode One Shot, choisissez un collimateur, PMC, bip et lumière de confirmation AF sur le collimateur choisi, shoot.
Hors situation où l'AI Servo est nécessaire, utilisez toujours le mode One Shot. Ainsi avec la confirmation de l'AF, vous saurez quand la MAP est faite et où vous l'avez faite.
4. "J'ai eu le bip et la lumière de confirmation AF, et quand je recadre, la mise au point se fait sur le fond, alors que j'ai gardé ma PMC sur le déclencheur"
Vous êtes en autofocus AI Focus. Un mode à banir absolument ! One Shot dans un premier temps, mais AI Servo ensuite, il décide donc tout seul quand garder la mise au point et quand basculer en autofocus continu. Aucun interet à l'utiliser, il vous fera rater vos recadrages à coup sûr. Pour du statique, One Shot. Pour du dynamique, AI Servo.
5. "On m'a dit de sélectionner One Shot, 1 seul collimateur, j'ai eu le bip de confirmation AF, et malgré ça, ma photo est floue !!!!"
Oui, car la vitesse utilisée est probablement trop basse pour figer votre propre tremblement ! Une règle empirique à mémoriser dit que pour éviter que votre propre tremblement floute la photo, il faut utiliser une vitesse d'au moins 1/focale. Ex: vous avez un 18-55mm utilisé à 55mm, il faut shooter au moins au 1/55. Pour plus de prudence, si vous êtes débutant et sur boitier APS-C, comptez le double, soit 1/100 environ. Évidemment, votre tremblement existe toujours, mais la durée pendant laquelle la photo est prise est tellement courte que ce mouvement n'a pas suffisament d'amplitude pour dépasser un pixel. Il ne se voit donc pas !
Le flou de bougé (caractéristique donc d'un mouvement) peut aussi être du à un sujet mobile. Cela peut être un effet voulu ou là encore, une déconvenue pour le photographe, mais il suscite rarement de question, étant beaucoup plus facilement compréhensible techniquement.
A noter que les objectifs IS repoussent cette limite, mais ne la suppriment pas. On peut ainsi shooter au 1/10 avec un 50mm par exemple, mais surement pas à 1/2s ou 1s !
Assurez vous également que le sujet n'est pas trop petit dans le viseur (comme un oiseau à bonne distance avec un téléobjectif "limité"). On ne peut pas demander à l'AF d'être hyper-précis sur un objet qui remplit 1% du cadre. L'AF sera hésitant et si la MAP see fait quand même, il n'y a aucune assurance qu'elle se soit faite pile sur la petite zone souhaitée, le resultat ne sera probablement pas net, vu les conditions dans lesquelles on l'a sollicité !! Il faut dans ce cas, ou se rapprocher, ou investir dans une plus longue focale (et souvent les deux !!).
A noter que selon certaines expérimentations, les MAP en intérieur seraient rendues plus difficile par les lampes flou-compactes (basse consommation) qui ont remplacé les bonnes vieilles ampoules à incandescence. Elles présenteraient un spectre avec peu d'infrarouges, infrarouges qui seraient particulièrement utile à l'AF. A confirmer toutefois.
6 "Quand je fais plusieurs fois la MAP en One Shot, ma photo est floue comme si la MAP avait varié entre chaque cliché, alors que mon sujet n'a pas bougé".
Il ne faut pas refaire la MAP quand elle est déjà faite. Ca oblige le boitier à recalculer une position, à faire bouger l'objectif alors qu'il est déjà bien calé et que la photo est nette, parce qu'il cherche desespéremment une meilleure MAP que la précédente. Résultat : la MAP peut être légèrement décalée. Quand le sujet n'a pas bougé, on ne refait pas la MAP, on garde le déclencheur à mi-course pour conserver la 1ere MAP et on déclenche autant de fois qu'on veut.
7. "Je ne comprends pas, j'ai sélectionné One Shot, 1 seul collimateur, mais l'autofocus patine, il n'accroche pas !"
Le module d'autofocus du boitier a besoin d'une zone suffisamment contrastée pour déterminer si c'est net ou pas. Pour simplifier et pour la compréhension, PMC, une séparation blanc/noir sur un mur blanc sera floue avant la MAP optimale et nette au moment où le point est fait. L'AF s'arrête. Bip et lumière de confirmation AF sur le collimateur choisi, shoot. Si on vise le mur blanc avec le même collimateur, il n'y aura pas assez de contraste pour que le boitier sache si la MAP est faite ou pas. En effet, du blanc flou et du blanc net, ça reste du blanc ! Ceci en théorie, car en pratique, les AF sont de plus en plus discriminants avec les petits détails (comme par exemple le crépis qui texture le mur) afin de faire quand même une MAP, mais rien n'est sûr. Le blanc, la visée à travers une vitre, des barreaux ou un grillage (zoo par exemple), le contre-jour sont autant de pièges pour l'AF, et donc la MAP n'est pas garantie. C'est pour ça qu'on peut encore faire une MAP manuelle de nos jours.
Évidemment, faire une MAP avec l'AF de nuit ou dans une ambiance très sombre (à l'intérieur) est très difficile aussi, et il faut parfois recourir à des objectifs ultra-ouverts (qui laissent rentrer beaucoup de lumière) ou à l'assistance du flash (et parfois aux deux !) pour réussir à faire une MAP.
Dans le même ordre d'idée, une atmosphère chargée en pollution, des courants d'air chaud, peuvent non seulement empêcher la MAP mais ôter toute netteté à un sujet éloigné, à cause de la couche d'air importante qui le sépare de l'objectif. Dans ce cas, une seule solution, dézoomer (moins grossir) ou (plus probable) attendre que les conditions atmosphériques soient meilleures. Il y a encore des photos qu'il est impossible de faire à un instant donné...
Vérifiez également que vous n'êtes pas en train de viser un sujet qui est en deçà de la distance minimale de mise au point de votre objectif. Celle-ci est spécifique à chaque optique. Ne vous approchez pas trop près afin d'éviter d'être au delà de la butée minimale de mise au point.
8. "Avec mon compact, tout était net et là, j'ai beaucoup de zones floues sur mon image."
Sur les compacts, la profondeur de champ (la zone de netteté avant et après la MAP) est très grande, par construction. Il est ainsi très difficile de détacher un sujet de l'arrière plan et voir un beau fond flou par exemple. Avec un reflex, c'est le contraire (et c'est d'autant plus vrai si l'ouverture est grande) ! Ainsi, il est naturel de ne pas avoir forcément l'ensemble de la photo nette. Ceux qui découvrent l'utilisation d'un objectif très ouvert et d'une focale moyenne comme le Canon EF 50mm F/1.8, expérimentent parfois la difficulté de gérer une PDC de quelques millimètres seulement à très grande ouverture. Pour simplifier, si l'on reste au même endroit pour shooter, la profondeur de champ est d'autant plus grande (/petite) que la focale est courte (/longue) et que le diaphragme est fermé (/ouvert).
La question est souvent posée pour des paysages à 18mm sur APS-C par exemple, où la mise au point est faite sur un avant plan très proche (souvent avec les collimateurs auto qui choisissent tout seul) et un diaphragme au maximum de l'ouverture. Avec un grand angle, une mise au point plus lointaine et un diaphragme plus fermé, et on obtient une photo nette de bord à bord.
9. "Avec mon compact, mes photos étaient très nettes. Avec mon reflex, même dans la zone de MAP, j'ai perdu en netteté, un comble !!"
Ici, on touche à une problématique qui n'est pas liée à l'optique mais au traitement des images. Un compact est réglé en usine pour délivrer des photos qui plairont au plus grand nombre, au très grand public, du petit cousin de 7 ans, à la grand mère de 77 ans. Et qu'est ce qui plait, au 1er coup d'œil ? Des photos qui ont "la pèche", avec du contraste, de la saturation, le ciel bien bleu, l'herbe bien verte, quitte à ce que ce ne soit plus très fidèle à la réalité. Et surtout pas mal d'accentuation (autrement appelée "netteté" ou "sharpening" en anglais). Le reflex, lui, est réglé d'usine avec des paramètres plutôt doux afin de permettre aussi de post-traiter si on le souhaite sur l'ordinateur. Mais si vous aimez les rendus des compacts, il suffit de pousser les curseurs "netteté" et "contraste" dans les menus de votre reflex, afin qu'il vous délivre d'emblée les images que vous souhaitez !
Autre chose (voir question 8), la moindre erreur de MAP sur un reflex se traduit par une perte de détails et dans certains cas, la PDC est de quelques millimètres seulement ! Ces erreurs de MAP sont souvent dues au fait que le photographe a bougé d'avant en arrière entre la PMC et le shoot.
10. "Les bords de ma photo sont moins nettes que le centre."
C'est classique, surtout à pleine ouverture. Les lois de l'optique étant ce qu'elles sont, les objectifs sont tous meilleurs au centre que sur les bords. Fermer un peu le diaphragme améliore souvent beaucoup la situation et comme d'habitude, les objectifs avec les optiques les plus haut de gamme sont beaucoup moins sensibles au phénomène.
A noter que cette caractéristique est tout à fait différente de la problématique de la profondeur de champ (question 7).
11. "Mes photos sur trépied sont moins nettes qu'à main levée"
Outre le problème de la stabilité (trépied de pacotille, trop léger, qui tremble au moindre coup de vent) et du déclenchement (si on veut déclencher de suite, un déclencheur souple est souhaitable. Sinon, on emploie le retardateur 2s ou 10s du boitier), il faut vérifier si votre objectif est stabilisé. En général, il est necessaire de désactiver l'IS qui, sur trépied, essaie de corriger un mouvement qui n'existe pas. Du coup, le moteur de l'IS crée un bougé préjudiciable à la netteté de l'image. Consultez toutefois le manuel de votre objectif : certains objectifs nouvelle génération détectent quand le boitier est monté sur trépied et coupent automatiquement l'IS. Cependant, prendre l'habitude de le désactiver soi-même évite de faire trop confiance à ces routines de détection.
12. "Je fais tout comme il faut et pourtant mes photos sont encore un peu floues. Mon objectif n'est pas du tout abimé, je l'ai même protégé avec un filtre !"
Classique aussi, le filtre de protection. Souvent de mauvaise qualité (car un filtre de qualité professionnelle coute parfois une centaine d'euros), le filtre rajoute une couche de verre, et une couche d'air (souvent chaud en plein soleil) devant l'objectif et peut générer des pertes de piqué ou de précision dans l'autofocus. Cet élément supplémentaire peut en plus souffrir de défauts de fabrication (verre, ajustage, etc...). Sauf utilisation en milieu hostile (plage, embrunts, projection d'eau ou de boue, etc...), il est préférable de monter le pare-soleil dédié, qui offre une bonne protection contre les chocs et même contre les projections (il faut que la projection arrive pile en face, puisque le pare-soleil protège les cotés), sans dénaturer les qualités de l'objectif et en améliorant le contraste (blocage des rayons lumineux incidents).
13. "Je suis toujours obligé de rajouter de la netteté sur mon PC dans mon logiciel de retouche ou dans Digital Photo Professional."
Sur votre boitier, faites attention de ne pas choisir le style d'image "neutre" qui est implanté pour permettre un maximum de post-traitement sur le PC. Le rendu est donc très doux (parfois limite flou, en tout cas suffisament pour croire qu'il y a un problème), sans aucune accentuation, car ce mode suppose que c'est vous qui dosez l'accentuation ensuite en post-traitement. Rien d'anormal à cela ! Donc, pour du jpg directement exploitable sans retouche de netteté, réglez la netteté de votre boitier à votre goût dans le style d'image : au minimum sur 3, voire sur 5 ou 6, et tout ira mieux. Ce réglage existe, ce n'est pas un péché de l'utiliser, c'est même prévu pour !
14. "Je n'arrive pas à obtenir une bonne netteté pour le visionnage sur mon écran. C'est embétant car je ne regarde mes photos que par ce biais !"
En cas de visualisation sur écran et dans ce but uniquement, n'hésitez pas à faire une version dédiée de vos photos afin que la définition de votre jpg corresponde à la définition de votre écran et à accentuer un peu le résultat de cette réduction afin de regagner le micro-contraste perdu dans le processus. Car dans ce cas, c'est vous qui avez la main sur l'ensemble de la procédure.
Laisser Windows/votre visualisateur faire cette réduction, c'est mal placer sa confiance. Comment est gérée la réduction à la volée pour l'affichage et l'anti-aliasing ? Y'en a-t-il ? Selon quelle méthode ? Et on se retrouve avec des photos molles, mal définies car réduites on-ne-sait-comment (c'est le cas de MSN par exemple, ou de la visualisation native de Windows XP).
Personnellement, je ne fais pas de version dédiée et j'utilise FastStone viewer pour mes affichages, qui me permet de choisir anti-aliasing ou non et selon quel méthode (lancsoz3 est la plus performante, sans mollesse induite, mais au prix d'un temps d'affichage un peu plus long).
J'ajoute au passage que la gestion de l'accentuation en post-traitement doit toujours se faire à 100% de la taille du JPG (donc après réduction à la taille de l'écran pour un jpg à voir par ce biais, ou à 100% de zoom pour les fichiers natifs JPG ou RAW sortis de la carte mémoire), jamais en version réduite "à la volée" par le logiciel (même Photoshop ou Digital Photo Professional), pour les raisons évoquées.
-
21/12/2009, 20h08 #3Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 [AIDE] Comprendre le trio vitesse/ouverture/ISO
[AIDE] Comprendre le trio vitesse/ouverture/ISO
Par Commoumou, d'après l'enseignement de Florent Doncourt, club photo de Metz.
 Envoyé par commoumou
Envoyé par commoumou
-
03/01/2010, 21h13 #4Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 [AIDE] Comment trouver ses fichiers RAW sur sa carte mémoire ?
[AIDE] Comment trouver ses fichiers RAW sur sa carte mémoire ?
Cette péripétie arrive très fréquemment par méconnaissance de son matériel ou de la procédure à suivre pour importer ses fichiers RAWs et nombre de débutants sur le forum posent régulièrement cette question.
1. Etre sûr que l'on peut enregistrer ses clichés au format RAW.
Certains appareils ne permettent d'enregistrer au format RAW que dans les modes dit "créatifs" (P, Av, Tv, M) et pas dans les modes "scènes" (portraits, paysage, sport, etc...). Verifiez dans votre manuel que le mode dans lequel vous prenez les photos vous permet bien d'enregistrer au format RAW.
2. S'assurer que l'on a bien réglé la qualité sur le format RAW.
C'est à dire en mode JPG + RAW (L+RAW, M+RAW, ou n'importe quelle combinaison de qualité JPG et d'enregistrement RAW) ou RAW seulement. L'utilisation de la qualité L seule ne fait qu'enregistrer un JPG. Inutile donc de chercher des RAWs sur votre carte !
Logiquement, si vous avez respecté 1) et 2), c'est sûr, vous avez des RAWs (fichiers .CR2, parfois .CRW pour les boitiers plus anciens) sur votre carte.
Comment les retrouver ? 2 solutions :
3. Vous ne disposez pas d'un lecteur de carte mémoire externe.
Il vous faut donc brancher votre boitier via le cable USB à votre ordinateur et (très important) importer les RAWs avec EOS Utility.
Si vous allez voir directement par l'intermédiaire de l'explorateur (en tout cas avec Windows XP) dans votre boitier branché en USB, Windows ne vous montrera que les JPGs (parce que les RAWs ne sont pas pour lui des "images"). C'est très souvent source de confusion puisqu'on a le sentiment qu'il n'y a pas de RAW sur la carte quand on regarde son contenu par ce biais !
4. Vous disposez d'un lecteur de carte mémoire externe.
Dans ce cas, rien de plus facile. Brancher votre lecteur, inserez votre carte mémoire. La carte est reconnue comme un disque dur externe (et uniquement dans ce cas), et vous pouvez parcourir son contenu avec l'explorateur, ou n'importe quelle application via le menu Ouvrir... par exemple. Vous y trouverez vos fichiers RAW et/ou JPG selon le paramétrage de qualité (question 2).
Question connexe, mais un peu hors-sujet :
5. "J'ai fait exactement comme expliqué au dessus. Et pourtant, je n'arrive pas à lire mes RAWs avec autre chose que Digital Photo Professional."
Certains boitiers peuvent enregistrer des fichiers RAW à plus faible définition, appelés mRAW ou sRAW. Ces fichiers RAW de qualité moindre ne sont souvent pas lisibles par des dérawtiseurs tiers. Il vous faudra donc peut être n'utiliser que Digital Photo Professional ou alors enregistrer des RAWs "plein format" pour pouvoir dérawtiser avec vos programmes favoris. Dans d'autres cas, même en utilisant le format RAW pleine définition, certains logiciels mettent du temps à se mettre à jour. Ainsi, les éditeurs mettent parfois quelques mois à prendre en charge les RAW des nouveaux boitiers. En attendant, une seule solution : DPP exclusivement !
J'espère que ces quelques questions/réponses vous permettront d'y voir plus clair et d'utiliser ce format facilement.
A+ sur le forum.
-
11/02/2010, 13h58 #5Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 [AIDE] Définition, résolution, DPI, taille, tirage...
[AIDE] Définition, résolution, DPI, taille, tirage...
Quelques définitions :
Taille : c'est la taille en cm (ou en mètres !) du tirage/impression
Définition : c'est la quantité de pixels en hauteur et largeur. Ex : 3888x2592 pour les capteurs 10MP. Pensez à la "haute définition" de la télé. C'est 1920x1080. Ce n'est pas la diagonale de la télé.
Résolution : ce sont les fameux DPI (Dot Per Inch = point par pouce). Soit la définition linéaire en pixels d'un coté divisée par la taille de sortie du même coté en pouces. Par exemple, 3888 pixels divisé par 30 cm de large soit ~12 pouces (1 pouce = 2,54cm) = 324 DPI. On dit qu'un périphérique, quel qu'il soit, a une grande résolution quand il est capable de capturer/restituer beaucoup de détails. C'est le cas aussi des scanners qui n'ont pas de "définition" en soi.
La résolution que vous pouvez lire ou enregistrer dans votre jpg avec votre logiciel de retouche n'a aucune espèce d'importance ! Pourquoi ? Parce que vous commandez un tirage d'une taille donnée (du 10x15cm, du 20x30cm, etc...) et le labo fait le tirage avec la définition du jpg que vous lui fournissez !!! Et peu importe la résolution enregistrée, votre 3000x2000 pxiels, qu'il soit inscrit 1 DPI ou 3000 DPI dans le jpg, le labo vous le tirera en 12x18cm par exemple, si vous avez commandé des tirages de cette taille.
Pour que les DPI enregistrés dans le fichier aient une importance, il faudrait que le labo lise la résolution dans votre jpg et qu'il tire en fonction, ce qui n'arrive jamais. On commande TOUJOURS une taille de tirage, non ?
Quelle taille de tirage pour quelle définition ?
Pour éviter de s'embrouiller, on peut diviser la définition par 100 pour connaitre la taille d'un tirage de bonne qualité. Exemple : 3000x2000 = 30xm x 20cm, ce qui donne 254 DPI, l'idéal communément admis est de 300 DPI. Pour les très grands tirages (poster), on les regarde de plus loin, donc on peut descendre. Regardez les affiches de pub en 4x3m et on voit les points à l'oeil nu
-
21/06/2010, 12h31 #6Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 [AIDE] Comment faire un micro-réglage de ses objectifs ?
[AIDE] Comment faire un micro-réglage de ses objectifs ?
Préalable :
MR = Micro-Réglages. MAP = Mise Au Point. AF = AutoFocus. PDC = Profondeur De Champ. CoC = Circle Of Confusion (cercle de confusion).
Les micro-réglages permettent de décaler logiciellement l'autofocus afin de corriger les front-focus (la netteté est devant la zone de mise au point) et back-focus (la netteté est derrière). Sous réserve d'un protocole rigoureux, elle permet de corriger les imperfections d'un boitier (correction globale) ou d'un objectif particulier.
Avant de procéder à un MR, assurez-vous que votre problème d'autofocus ou de netteté n'est pas décrit ici.
J'attire votre attention sur le fait que cette fonctionnalité est une "béquille", elle ne remplace pas un vrai réglage de l'autofocus, fait par un atelier Canon.
J'ai noté une baisse assez nette de la précision de l'AF en lumière tungstène/basse conso, problème assez connu quel que soit la marque sur les forums anglo-saxons (chercher "focus shift artificial light" dans google) et connu aussi de Canon puisqu'il en est fait mention dans le "white paper" du 50D/5DmkII avec un autofocus qui est censé détecter le type de lumière et faire une correction exploitant la puissance du Digic IV. Je lis bien peu de choses à ce sujet en français et ici sur le forum. Aussi, je vous recommande de faire vos tests de MAP en lumière du jour, et pas en lumière artificielle, ce qui expliquerait certains A/R répétés au SAV et l'incompréhension qui s'en suit.
Mise en oeuvre :
L'idée est de tester uniquement les erreurs d'AF dans des conditions de prise de vue idéales. Il faut éliminer toute autre source d'erreur. Donc, appareil parfaitement fixe (pas de risque de bougé), avec une excellente lumière (pas de problème de détection de contraste), sur un sujet suffisamment large pour englober la totalité du capteur AF (les dessins des collimateurs AF ne représentent pas fidèlement l'emplacement des capteurs AF). Ça veut dire (et ça n'engage que moi) : pas de mire à 45° (avec une ligne tellement fine qu'on ne peut jamais être sur que le capteur a correctement réagit dessus), mais des cibles perpendiculaires à l'axe optique de l'objectif, comme les sujets que l'on photographie. Il y a trop de possibilités d'erreur avec une mire à 45° artisanale pour faire précisément à domicile ce genre de réglage. Une fois la précision des résultats assurés via une méthode fiable, le réglage est facile puisqu'il suffit de comparer sur les clichés quel réglage est le meilleur.
Donc, la méthode que j'utilise (et dont je ne revendique aucunement la paternité, ayant été popularisée dans les forums par d'autres) est celle des bouteilles/livres/DVD décalés. En l'occurrence, ici, ce seront des paquets de pâtes. Qu'importe la cible, il faut qu'elle soit bien éclairée, pas trop brillante afin d'éviter les reflets et qu'elle comporte des zones avec des motifs sur lesquels l'AF puisse se caler (pas de cibles unies).
Je place sur le même plan l'appareil photo et les mires, à la distance de 50x la focale de l'objectif testé. Une variante pour les longues focales peut être la distance de MAP d'usage, si la longueur de test est vraiment trop importante (au passage, cette distance de 50x la focale, recommandée par Canon, invalide également la méthode de la mire à 45°, car on arrive pour un simple 50mm à une distance de 2,50m entre la cible et le capteur, soit un appareil à 45° sur trépied à 1,76m de hauteur, avec la mire au sol, ce qui exclut les tests et réglages d'objectifs longs avec cette méthode).

Ici sur un buffet, pas de problème (distance 50x 35mm soit 1,75m), mais on peut imaginer placer les cibles sur une table, et placer l'appareil sur trépied (à la condition qu'il soit capable de supporter le poids de l'ensemble boitier-objectif, c'est indiqué dans la documentation du trépied) à la même hauteur, en s'étant assuré de l'horizontalité avant-arrière (le tangage pour les marins) avec un niveau à bulle. A l'extrême, la mise en place du dispositif au sol est possible, mais ne facilite pas la visée.
L'appareil photo est en place, parallèle aux cibles (ici le bord du buffet m'aide évidemment, mais on peut aussi se fier quand on est sur trépied au carrelage au sol ou à l'alignement par rapport au mur derrière). Même si l'appareil n'est pas parfaitement horizontal et parallèle aux cibles, il faut par contre qu'il soit absolument fixe. Une erreur de quelques degrés ne se voit pas sur les clichés (dont la profondeur de champ est toujours suffisante) et l'étude par comparaison de clichés réalisés dans les mêmes conditions permet de s'affranchir de ce biais.
Réglage du boitier :
Techniquement, afin de mesurer la précision de l'AF dans les pires conditions (c'est à dire avec la profondeur de champ minimale), j'utilise le mode Av et la pleine ouverture (ici F/2). Je m'assure, même si l'appareil photo est stable, d'une vitesse égale à 2 ou 3x la focale (en l'occurrence 1/100 pour un 35mm). Ne pas hésiter à recourir à des éclairages supplémentaires type lampe de bureau, pour éclairer les cibles afin d'augmenter la vitesse d'obturation et faciliter l'efficacité du module AF. Dans mon cas, l'appareil est dos à une fenêtre. On utilisera un déclencheur souple ou le retardateur 10s. l'IS sera désactivé afin d'éviter les flous de bougés. Le style peut être réglé indifféremment. Personnellement, je reste sur "Standard" (pas de netteté 0 car pour le coup, la netteté optimale serait difficile à évaluer). Évidemment, les filtres UV, neutre ou polarisant seront retirés. L'AF sera réglé sur One Shot. On selectionnera uniquement le collimateur central et il sera largement recouvert par la cible du milieu dans le viseur (pas d'AF spot, si on a un 7D/1D).

(qualité médiocre de ce cliché du viseur, mais l'essentiel y est).
Au passage, la visée se fait dans le viseur, pas en LiveView puisqu'on cherche à calibrer les capteurs AF, précisément ceux qui sont utilisés lors de la visée à l'œilleton. Le LiveView permet soit de faire le point en calculant le contraste directement sur le capteur (méthode lente mais silencieuse) sans la participation des capteurs AF qui nous intéressent, soit de faire le point avec les capteurs AF après un aller-retour miroir (méthode rapide mais bruyante) mais sans pouvoir vraiment sélectionner celui qui la fait (le rectangle affiché sur l'écran décrit la zone, mais pas le capteur utilisé).
Placement des cibles :
Les cibles sont décalées afin de percevoir le décalage de mise au point. J'utilise le logiciel freeware Barnack pour calculer la PDC du cliché, car les caractéristiques de chaque boitier me semblent plus complètes que sur dofmaster.com (pour lequel par exemple, tous les APS-C disposent du même réglage de cercle de confusion, sans tenir compte de la densité de pixels), mais le principe reste le même. Une traduction en francais est disponible ici (merci à BNCSC pour l'info). Attention : La boite "35mm CoC Reference" doit contenir la valeur 0,030 puisqu'elle traduit la valeur du CoC au format 35mm autrement appelé 24x36... Ne changez jamais cette valeur (les données de calcul sont mise à jour avec la selection du boitier).
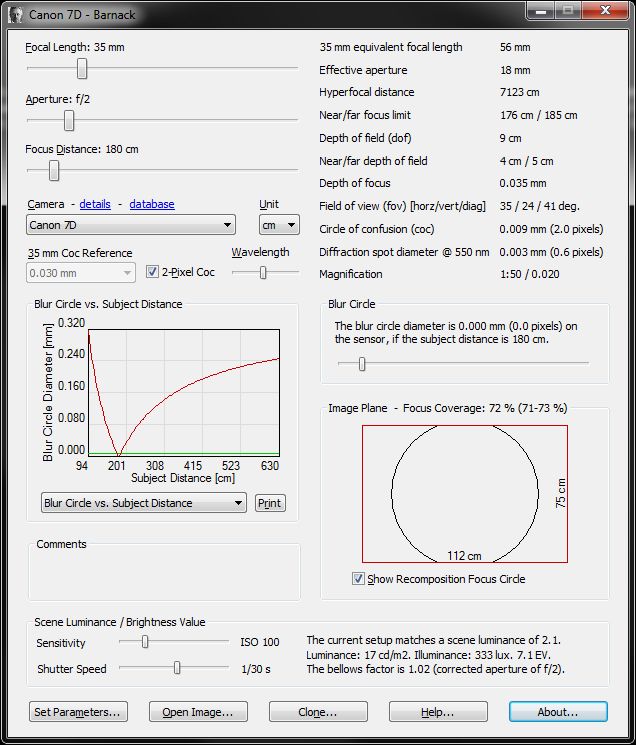
Pour un cliché à 35mm et 1m80 à F/2 et un cercle de confusion correspondant à la distance entre 2 pixels (je préfère cette valeur à un CoC classique de 0,019mm), j'obtiens une profondeur de champ d'environ 5cm devant et derrière le point. Je décale donc mes cibles d'autant. Ainsi, en théorie, si la MAP est parfaite sans besoin de MR (réglage sur 0) sur la cible du milieu, je devrais percevoir la fin de la PDC sur la cible à l'arrière et le début de la PDC sur la cible à l'avant du cliché. Cet écart conditionne la précision de la mesure. Si vos cibles présentent à peu près la même netteté sur le 1er cliché test, augmentez le décalage. Si les cibles de part et d'autre de la cible centrale sont vraiment trop floues, réduisez le décalage. Disons que le calcul de Barnack permet d'avoir une base.

Méthode de réglage :
Une fois tout ce petit monde en place, on a finalement fait le plus dur.
2 méthodes pour prendre les clichés. Cependant, chaque cliché devra se faire avec une MAP déréglée, vers la MAP minimale (personnellement, je mets ma main devant l'objectif, afin d'éviter de toucher au boitier et je fais une pression à mi-course sur le déclencheur). Pour plus d'assurance, certains conseillent de tripler chaque cliché sur un seul MR, afin d'éliminer les petites variations de MAP et d'éviter d'éliminer trop vite un bon MR (ceci est particulièrement vrai sur les objectifs non USM, dont le moteur par construction est moins précis). La comparaison se fera dans le logiciel de votre choix, à la condition de toujours comparer les clichés à un grossissement de 200%.
La méthode "en finesse" : il faut déclencher une première fois avec le MR à 0. Regarder ensuite quelle cible, la plus près ou la plus loin, est la plus nette. Si c'est la plus loin (près), on corrigera à +5 (-5) par exemple, on refait un cliché et on compare avec le 1er. Si le décalage s'est réduit, mais est toujours présent, il faudra amplifier la correction par exemple à +10 (-10). Si le décalage s'est inversé, si c'est désormais la plus près (loin) qui est nette, il faudra par exemple appliquer un +3 (-3), etc...
Avantage : permet de trouver plus vite le bon réglage.
Inconvénient : en cas d'erreur, il faut refaire la procédure, c'est du coup parfois plus long et les allers-retours devant le PC pour voir dans quel sens faire la correction peuvent être fastidieux.
La méthode "brutale" : là, c'est simple, on déclenche avec un MR à -20, puis à -19, -18, etc... (soit 40 clichés) et on compare sur son PC, cliché après cliché, afin de trouver lequel est le meilleur et on en déduit le MR adapté.
Avantage : on dissocie les 2 séquences prise de vue et lecture sur le PC, c'est plus confortable.
Inconvénient : on est obligé de shooter 40x (ou 120x si on triple chaque cliché).
Personnellement, je fais un mélange des deux. Je shoote à -20, -10, 0, 10 et 20 et je cerne la fourchette de valeur qui semble contenir le bon MR. Je fais ensuite 10 clichés en changeant à chaque fois de MR dans cet intervalle.
A noter : la valeur du MR est présente dans les EXIFs du cliché, quand vous le lisez avec DPP, dans le fenêtre de propriétés de l'image (Ctrl I).
Souvent, 2 valeurs de MR sont bonnes et on ne voit aucune différence même à fort niveau de grossissement. Dans ce cas, il vaut mieux choisir le MR le plus petit, les objectifs et leur moteur s'accommodant mieux d'un micro-front-focus. Ex: les 2 JPGs sont aussi bons avec un MR de +4 et de +5. On choisira donc le MR de +4.
Si vous n'arrivez pas à trouver le bon MR, ou si vous avez la sensation qu'il est plus "loin" que +20 ou -20, il faudra envoyer votre boitier et vos objectifs Canon au SAV (Si vous utilisez des objectifs Sigma, Tamron ou Tokina, les techniciens Canon n'y toucheront pas, il faudra renvoyer vos objectifs vers leur SAV respectif, sans le boitier).
J'espère avoir éclairci certains points et fourni une méthode relativement facile à mettre en œuvre, en éliminant au maximum les aléas afin d'obtenir un réglage le plus fiable possible.
-
01/07/2010, 21h36 #7Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 [AIDE] Obtenir une profondeur de champ maximale en utilisant la distance hyperfocale
[AIDE] Obtenir une profondeur de champ maximale en utilisant la distance hyperfocale
Préalable :
MAP = Mise Au Point. PDC = Profondeur De Champ. DH = Distance Hyperfocale
En paysage (mais pas exclusivement), on recherche souvent la profondeur de champ maximale (c'est à dire la zone qui apparait comme nette devant et derrière l'endroit où a été fait la mise au point). Intuitivement, on se doute qu'il faut fermer le diaphragme pour l'obtenir. Oui, mais fermer à combien ? F/8 ? F/16 ? Fermer pareil à 17mm ou à 50mm ? Comment obtenir la PDC la plus large possible ? Pour cela, il faut connaitre une donnée optique primordiale pour cet exercice : la distance hyperfocale.
Définition
La distance hyperfocale (souvent appelée par abus de langage et à tort "hyperfocale" tout court, mais il s'agit bien d'une distance !) est définie comme :
- La distance nette minimale au delà de laquelle tout est net jusqu'à l'infini quand la MAP est à l'infini. En clair, on fait la MAP sur l'infini et on est net depuis la DH jusqu'à l'infini.
- La distance sur laquelle la MAP doit être faite pour obtenir une PDC allant de la moitié de la DH jusqu'à l'infini. En clair, on fait la MAP sur la DH et on est net depuis la moitié de la DH jusqu'à l'infini
Avec quel objectif ?
A partir de là, la méthode à utiliser va dépendre des objectifs que vous possédez.
Si vous possédez des objectifs qui comportent des repères de mise au point avec une fenètre des distances, vous pourrez faire la MAP sur la DH ou sur l'infini.
Si vous possédez des objectifs qui ne comportent pas ces repères, vous ne pourrez faire la MAP que sur l'infini (en visant un objet lointain en One Shot). On peut en théorie faire la MAP sur un objet qui est à la distance hyperfocale par rapport au boitier. Mais ça impliquerait de mesurer précisément cette distance (gare au piège, voir ci-après).
En pratique, l'optimisation de la PDC ne peut donc se faire qu'avec des objectifs avec cette fenêtre des distances, pour faire coïncider le repère de MAP avec la DH que l'on aura calculée. Les autres, avec le même boitier, la même focale, la même ouverture, perdront à chaque fois, la moitié de la DH en profondeur de champ, à cause de leur impossibilité à régler précisément manuellement la MAP sur la DH. Cela dit, ils pourront quand même connaitre précisément les réglages qui leur permettront la PDC maximale avec leur matériel.
Calcul de la distance hyperfocale
J'utilise le logiciel freeware Barnack pour calculer la PDC du cliché, car les caractéristiques de chaque boitier me semblent plus complètes que sur dofmaster.com (pour lequel par exemple, tous les APS-C disposent du même réglage de cercle de confusion, sans tenir compte de la densité de pixels), mais le principe reste le même. Une traduction en francais est disponible ici (merci à BNCSC pour l'info). Je règle le cercle de confusion correspondant à la distance entre 2 pixels (je préfère cette valeur à un CoC classique de 0,019mm). Attention : La boite "35mm CoC Reference" doit contenir la valeur 0,030 puisqu'elle traduit la valeur du CoC au format 35mm autrement appelé 24x36... Ne changez jamais cette valeur (les données de calcul sont mise à jour avec la selection du boitier).
Ainsi, on règle, la focale, l'ouverture choisie, et on obtient la distance hyperfocale :
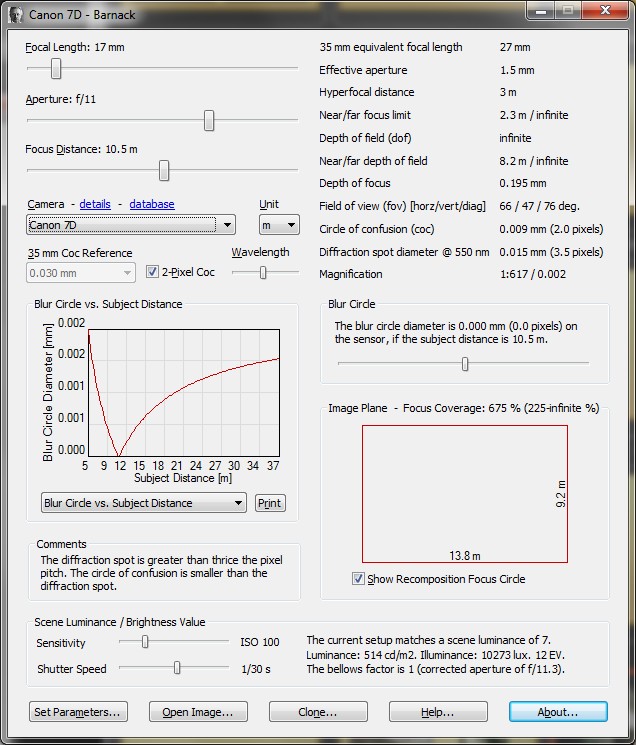
Pour 17mm sur un 7D, à F/11, la distance hyperfocale est à 3m. Plus on ferme, plus la DH est proche. Plus la focale est courte, plus la DH est proche. Elle n'est fonction que de la focale et de l'ouverture. Elle ne change pas avec la distance de mise au point.
Donc, si je peux, je fais une MAP manuelle en plaçant le repère en face de 3m et j'ai de facto une PDC qui va de 1,5m à l'infini. Si mon objectif est dépourvu de repère de distance, en faisant la MAP à l'infini, je sais que je serais net de 3m à l'infini.
On peut faire une table de DH, mais en pratique, je ne retiens que quelques distances seulement, en fonction de mes habitudes. Par exemple, je sais qu'à 10mm et F/11, la DH est à 1m, ce qui assure une PDC quasi totale quelque soit l'endroit où se trouve mon sujet.
Application de la méthode de la distance hyperfocale
- Savoir quel valeur de diaphragme adopter afin d'éviter de "visser" inutilement (fermer) le diaphragme (à F/22 voire plus) et faire apparaitre la diffraction, qui dégrade la netteté du cliché.
- Optimiser sa profondeur de champ et obtenir avec certaines combinaisons de focales et d'ouverture une PDC quasi totale, qu'on n'obtiendrait que par tatonnement sans connaitre les dessous de la technique et le calcul exacte de la DH.
- Pouvoir s'affranchir de la mise au point, pour une réactivité maximale, en reportage par exemple. Ainsi, avec une focale reportage (22mm sur APS-C ou 35mm sur 24x36) à F/16 et en préréglant la MAP sur la moitié de la DH, on obtient une PDC très confortable en ayant fait la MAP une fois pour toute et les prises de vue se font sur le vif, sans devoir attendre que l'AF accroche quoi que ce soit. C'est aussi comme ça que sont pris les clichés grand-angle derrière les buts lors des matchs de football avec des boitiers télécommandés avec une MAP fixe sur la DH.
Le Piège
Le piège, c'est de régler sa MAP incorrectement sur la DH, c'est à dire en réalité sur une distance inférieure à la DH. Ex: la DH est à 3m et je règle la MAP avec mon repère de distance à "pas-tout-à-fait 3m". La MAP est en fait à 2m, on perd instantanément la PDC jusqu'à l'infini !!! On aura donc tendance à régler sa MAP un peu plus loin que la DH afin de conserver une marge de sécurité. Ce qu'on perd en optimisation, on le gagnera en sérénité !
Aide au calcul sur le terrain
(d'après l'article de Réponse Photo n°223)
On peut calculer sur le terrain assez facilement sa distance hyperfocale avec le nombre K (appelé NK). Par analogie avec le NG (nombre guide du flash), ce nombre divisé par le diaphragme donne la distance hyperfocale. Très bien, sauf que NK est dépendant de la focale... Pour les zooms, il faut donc un petit tableau où on a autant de NK que de focales... En pratique, on le calculera essentiellement sur les focales grand-angles de son zoom. Aucun problème avec les focales fixes évidemment.
Pour le calcul, c'est relativement simple (je passe rapidement sur la démonstration, tout part de la définition mathématique de la DH). Il s'agit de la focale au carrée divisée par le CoC (0,019 pour l'APS-C, 0,03 pour le 24x36 ou le "2-pixel CoC" de Barnack). Divisez ensuite par 1000 pour convertir les mm en mètre.
Par exemple, pour un 10mm sur APS-C, on obtient 10x10/0,019= 5263. Soit divisé par 1000, 5,26. Arrondissons par excès à 6 pour que ce soit pratique sur le terrain et que l'on soit sur de ne pas être en deça de la DH lors du réglage (voir le paragraphe "le piège").
On divise ensuite simplement ce NK par l'ouverture et on obtient la DH.
Ainsi, dans l'exemple, à F/2, l'hyperfocale sera à 3m. A F/5.6, juste au dessus du mètre (6/5.6=1,07m). A F/10, à 0,60m.
Sur mon image d'illustration, avec les réglages de la capture d'écran, on calcule un NK à 17x17/0.009 puis divisé par 1000, égal à environ 33. Et divisons 33 par 11, on obtient 3m, ce qui est du coup le résultat du calcul précis de la DH.
A noter que pour les allergiques au calcul, il suffit de demander à n'importe quel logiciel de calcul d'hyperfocale (Barnack et les autres) la DH à F/1. Il s'agit par définition du nombre NK.
-
20/09/2010, 16h03 #8Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 [AIDE] Comprendre le fonctionnement de la cellule d'exposition
[AIDE] Comprendre le fonctionnement de la cellule d'exposition
Définition de l'exposition
C'est la quantité de lumière reçue par le capteur. Elle est dépendante de la triade vitesse/diaphragme/ISO. Une bonne exposition est celle qui permet de rendre correctement une scène. Le problème, c'est que l'oeil a une dynamique (la capacité à rendre les nuances) qui est bien supérieure à celle d'un capteur numérique... Il faut donc connaitre le fonctionnement d'une cellule d'exposition pour l'anticiper et la corriger si nécessaire.
Rappel des modes de mesures
Evaluative [(●)] : Cette mesure prend en compte la totalité de l'image au moyen d'un catalogue de clichés intégrés dans la mémoire du boitier. La cellule compare la situation actuelle avec une situation similaire de la base de donnée et en déduit les réglages d'exposition mais un poids plus important est accordé au collimateur actif dans le calcul. C'est le seul mode qui conserve la mesure lors du recadrage en gardant le déclencheur à mi-course.
Selective [( )] : Cette mesure ne prend en compte que la partie centrale du viseur. Mémorisation obligatoire lors d'un décadrage par la touche *.
Spot [ ● ] : Cette mesure ne prend en compte qu'une zone très restreinte au centre du viseur (quelques %). Mémorisation obligatoire lors d'un décadrage par la touche *.
Pondérée [__] : Cette mesure accorde plus de poids au centre de l'image, et fait la moyenne avec l'ensemble de l'image. Mémorisation obligatoire lors d'un décadrage par la touche *.
Le mode de calcul de la cellule d'exposition
La cellule d'exposition, quelque soit le mode choisi (evaluative, selective, spot ou pondérée), est "stupide"... Elle calcule les paramètres d'exposition (tous, certains ou aucun en fonction des modes utilisés : mode scène, P, AV, Tv, ou M) pour que la "luminosité" de la photo soit la même que le fameux "gris 18%", qu'on retrouve sur les chartes de mesure, que l'on peut acheter dans le commerce.
Ainsi, une zone très blanche sur laquelle on fait la mesure, sera interprétée comme une zone grise très très très éclairée. En conséquence, la mesure étant trompée, elle tentera de corriger une fausse impression, cette zone sera rendue grise sur le cliché, donc sous-exposée.
Au contraire, une zone très sombre sur laquelle on fait la mesure, sera interprétée comme une zone grise très très très peu éclairée. En conséquence, la mesure étant trompée, elle tentera de corriger une fausse impression, cette zone sera rendue grise sur le cliché, donc sur-exposée.
C'est ainsi qu'il faut faire une correction d'exposition positive (donc sur-exposer par rapport au calcul) quand on fait la mesure sur un mur blanc en plein soleil ou sur un paysage de neige. A l'inverse, il faudra corriger négativement (donc sous exposer), une photo en fin de soirée, si l'on ne veut pas avoir l'impression qu'elle a été prise en plein après-midi.
On prendra donc garde à ne pas placer le collimateur actif n'importe où, même (et surtout !) en mesure évaluative, ou alors à faire une correction adaptée, voire les deux ! Exemple, sur un sujet en t-shirt blanc, on aura intérêt même en évaluative à faire la mesure avec le collimateur actif sur le visage de personne, et même à appliquer une correction pouvant aller jusqu'à 1 IL (prise en compte de l'ensemble de la photo). En mesure spot, la mesure sur le visage devrait suffire à donner une bonne exposition du cliché. Sur une photo de paysage, le collimateur en mesure évaluative aura tout intérêt à ne pas être placé dans une zone à l'ombre, sinon le reste de la photo risque d'être sur-exposé, etc...
La quantité de correction dépend de la cellule (le "calage" de la mesure peut être différent selon les boitiers) et du risque que l'on consent à courir (risque de crâmage des blancs). Dans le cas d'une robe de mariée en plein soleil, on évitera d'aller trop loin si on ne connait pas bien la limite de son matériel par exemple (instants à ne pas rater). Dans le cas d'un paysage, on aura le loisir de faire sa mesure à différents endroits et avec différentes corrections afin de comprendre les réactions de la cellule et de trouver la bonne exposition.
A noter que le crâmage des hautes lumières (on parle parfois de hautes lumières "percées") se détecte ou sur l'histogramme (histogramme tassé à droite) ou grâce au clignotement des zones sur-exposées sur l'écran au dos du boitier (fonction désactivable, vérifiez votre paramétrage).
Évidemment, la correction d'exposition ne s'entend qu'en P, Av, et Tv (symbole Av +/- sur le boitier ou la roue codeuse des boitiers experts). En mode M, l'exposition sera réglée manuellement, mais le barre-graphe dans le viseur rendra compte de l'écart entre l'exposition selon les choix du photographe et le calcul de la cellule : la correction à appliquer se fera donc en diminuant/augmentant vitesse, ISO, ou diaphragme.
"Sur certaines photos, je n'arrive pas à obtenir une bonne exposition. Il y a des zones bouchées ou alors des zones crâmées. Comment obtenir un cliché où tout est correctement exposé ?"
C'est difficile. La situation décrite correspond à un écart entre hautes lumières et basses lumières qui dépasse la dynamique du capteur (cas par exemple d'une photo en sous-bois avec des percées de lumière ou du plus classique contre jour). Si on expose correctement les ombres, les hautes lumières seront crâmées. Si on expose pour les hautes lumières, les ombres seront sans détails.
Dans cette situation, photographier en RAW est un énorme avantage, vu le nombre d'informations stockées dans ce type de fichier (beaucoup plus que dans un JPG). Il sera donc beaucoup plus facile à travailler.
1er solution : le HDR (High Dynamic Range). En résumé, prendre plusieurs clichés avec des expositions différentes, afin d'enregistrer par exemple 1 cliché pour les hautes lumières (avec donc la mesure d'exposition faite sur cette zone), 1 cliché pour les tons moyens, et 1 cliché pour les ombres. Fusionnés au moyen d'un logiciel (Photomatix, EasyHDR, mais aussi au moyen de calques sous Gimp ou Photoshop), ces clichés permettent d'étendre la dynamique et produisent une photo que le boitier aurait été incapable de capturer en une seule fois. Attention, les 3 clichés ne doivent différer que par leur exposition (pas de sujet en mouvement, cadrage strictement identique) et nécessitent donc l'emploi d'un trépied.
2e solution : le "pseudo-HDR". Ici, on s'attache à remplir au maximum l'histogramme (des tons sombres aux hautes lumières), afin d'optimiser la dynamique du capteur sur un seul cliché. On remonte ensuite les ombres et on assombrit les hautes lumières lors du développement du RAW, format obligatoire pour utiliser cette technique. Avantage : 1 seul cliché, photographier un sujet en mouvement est donc possible, pas de trépied, mais la dynamique finale est évidemment inférieure au résultat de la fusion de 3 clichés et la remontée des ombres en post-traitement rend le bruit numérique plus visible. Faibles ISOs très recommandés !
3e solution : le flash ou toute autre source d'appoint (comme un réflecteur par exemple). On réduit ainsi l'écart de luminosité entre avant-plan et arrière plan, et tous les tons de la photo sont cette fois saisis grâce à la dynamique du capteur. C'est le fameux "débouchage des ombres" ou "fill-in". Pour l'utiliser, mode Av (qui pose pour l'arrière plan) + flash (qui exposera pour l'avant-plan). Évidemment, pour utiliser cette technique, il faut que le sujet soit à portée de flash, ce qui exclut les paysages, par exemple.
"J'ai réglé la correction d'exposition à +1 sur l'écran, mais dans le viseur, le barre-graphe ne rend pas compte de cette correction."
Attention de bien avoir réglé la fonction Av +/- et pas la fonction +/- ! La correction d'expo flash induit une sur-exposition ou une sous-exposition de l'éclair, mais ne modifie pas les calculs de l'exposition faits par la cellule. Il existe sur certains modèles de boitier un rappel au moyen d'une icône dans le viseur, qui indique que la correction d'expo flash est non nulle.
+/- ! La correction d'expo flash induit une sur-exposition ou une sous-exposition de l'éclair, mais ne modifie pas les calculs de l'exposition faits par la cellule. Il existe sur certains modèles de boitier un rappel au moyen d'une icône dans le viseur, qui indique que la correction d'expo flash est non nulle.
Par contre, n'utilisez JAMAIS la fonction "correction automatique de luminosité" !! Cette béquille triture votre photo et corrige à votre insu vos erreurs d'exposition. Très bien me direz vous ! Sauf que ce faisant, il est impossible de comprendre comment l'exposition est gérée par la cellule, et qu'évidemment, cette correction a des limites, et en particulier la montée du bruit, qui arrive très très vite, dans les zones sous-exposées, mais corrigées par le boitier. Il convient donc de la desactiver, de savoir pourquoi la photo est sous-exposée, et de corriger en conséquence. J'ajoute que pour ceux qui utilisent le format RAW, le JPG affiché au dos du boitier tient compte de cette correction et vous risquez de prendre pour "bien exposée" une photo qui est mal exposée. Or cette correction ne se voit et ne s'utilise que dans Digital Photo Professional (on peut toutefois la décocher à la demande si vous l'avez paramétrée sur le boitier), et les autres dérawtiseurs n'en tiennent pas du tout compte ! Vous vous retrouvez donc avec une photo sous-exposée (ce qu'elle est à l'origine) alors que l'histogramme au dos du boitier était apparemment correct.
-
29/05/2011, 11h54 #9Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 Préparer ses photos pour EOS-numerique
Préparer ses photos pour EOS-numerique
Il est fréquent que certains membres ne prennent pas le soin de traiter leur photo pour un affichage web, que ce soit sur un site personnel, et évidemment sur EOS-numerique, avec les contraintes de définition (en pixels) et de poids (en ko) expliquées dans ce post. Car il ne suffit pas de faire une bonne photo, il faut ensuite savoir comment bien la présenter sur un site web, afin de lui rendre grâce. J'espère que ce tuto vous aidera à préparer au mieux vos clichés.
"Pourquoi ai-je besoin de préparer mes photos ?"
Réduire une image qui fait 6, 8, 10, 15 ou 18 mega-pixels fait appel à un algorithme de redimensionnement. Certains logiciels permettent de choisir une méthode parmi plusieurs, d'autres non. Mais beaucoup de méthodes provoquent une mollesse de l'image en réduisant la définition de manière aussi sévère. C'est pourquoi après le redimensionnement, il faut appliquer une accentuation (parfois un peu abusivement appelée netteté). Accentuation, parfaitement absente, quand on se contente d'afficher son image en plein écran, la redimensionnement se faisant "à la volée", et dépendant du logiciel utilisé (DPP, Aperçu Windows, etc...). Certains algorithmes sont toutefois prévus pour les redimensionnements pour le web, comme le "Bicubic Sharper", disponible dans Adobe Photoshop quand on choisit la méthode de réduction, mais pas dans les logiciels grand public.
Les logiciels les plus simples n'offre qu'un type de réglage (une seul réglette, de 0 à 10, par exemple), c'est néanmoins suffisant pour ce qui nous interesse dans ce tuto. D'autres plus évolués offrent la triade classique pour l'accentuation, à savoir l'intensité (aussi appelé gain), le rayon exprimé en pixels, et le seuil. Pour faire simple, cette accentuation applique une fine bande de pixels clairs en bordure des pixels foncés, et une fine bande de pixels foncés en bordure des pixels clairs. L'intensité détermine la visibilité de la bande (un peu comme si l'accentuation était plus ou moins transparente sur l'image). Le rayon correspond à la largeur de la bande (c'est pour ça que l'unité de ce paramètre est le pixel plutot qu'un pourcentage). Le seuil détermine la limite en deçà de laquelle l'accentuation ne s'applique pas, comme par exemple, les zones floues à l'arrière plan ou les applats de couleurs, dans lesquels une accentuation trop poussée fait remonter le bruit en haute sensibilité.
"Quels réglages dois-je adopter ?"
Difficile de répondre avec une recette universelle pour tous les utilisateurs. Cela dépend de vos gouts mais aussi de la définition de l'image initiale. Réduire une image de 300D de 3072px de coté, en une image de sortie à 1000px, divise le nombre de pixels du grand coté par 3. Les 5616px d'un 5D mark II seront eux presque divisés par 6, soit le double de la perte avec un 300D !! On ne peut donc pas accentuer de la même façon 2 fichiers de 2 boitiers différents ! Le mieux est de faire des essais. Il est toutefois préférable de se concentrer sur l'intensité, le rayon devant de toute manière rester faible (pas plus de 1 pixel) sur un fichier de très basse définition.
"Quel logiciel dois-je utiliser ?"
Tous les logiciels de manipulation de photos permettent de réduire une image et de l'accentuer. Beaucoup obligent à traiter les images une par une. Certains permettent un traitement par lot.
Je vous propose un exemple avec FastStone Viewer, logiciel très complet de visualisation/diaporama avec des fonctions de retouches basiques mais suffisantes pour la plupart des utilisateurs (saturation, contraste, etc...) et un autre exemple avec BorderMaker, logiciel dédié au traitement par lot de tout un répertoire. Cependant, c'est la trame générale qui est importante, la marche à suivre étant toujours la même, et reproductible dans l'interface de n'importe quel logiciel, à quelques détails près.
Avec FastStone Viewer
Téléchargeable ici : Download FastStone Image Viewer (freeware)
Ouverture en plein écran (j'ai simulé sur mon écran un définition de 1024x768) d'une image de 18MP :

Le menu s'ouvre à gauche en passant la souris dessus :
Clic sur Redimensionner et cette fenêtre s'ouvre.
On rentre 1024px en largeur en s'assurant que la case "Conserver les proportions" est bien cochée. FastStone Viewer propose plusieurs méthodes de redimensionnement. De mes vagues essais, j'en ai déduit qu'il n'y avait pas beaucoup de différences entre elles... Je conserve donc la méthode par défaut, Lanczos3.
Affichage désormais de l'image réduite, en pleine écran, mais où donc 1 pixel de l'image correspond à un pixel de l'écran. Vous remarquerez d'ailleurs que le niveau de zoom est désormais de 100%. Ouvrons le menu à gauche et choisissons "Netteté/flou".
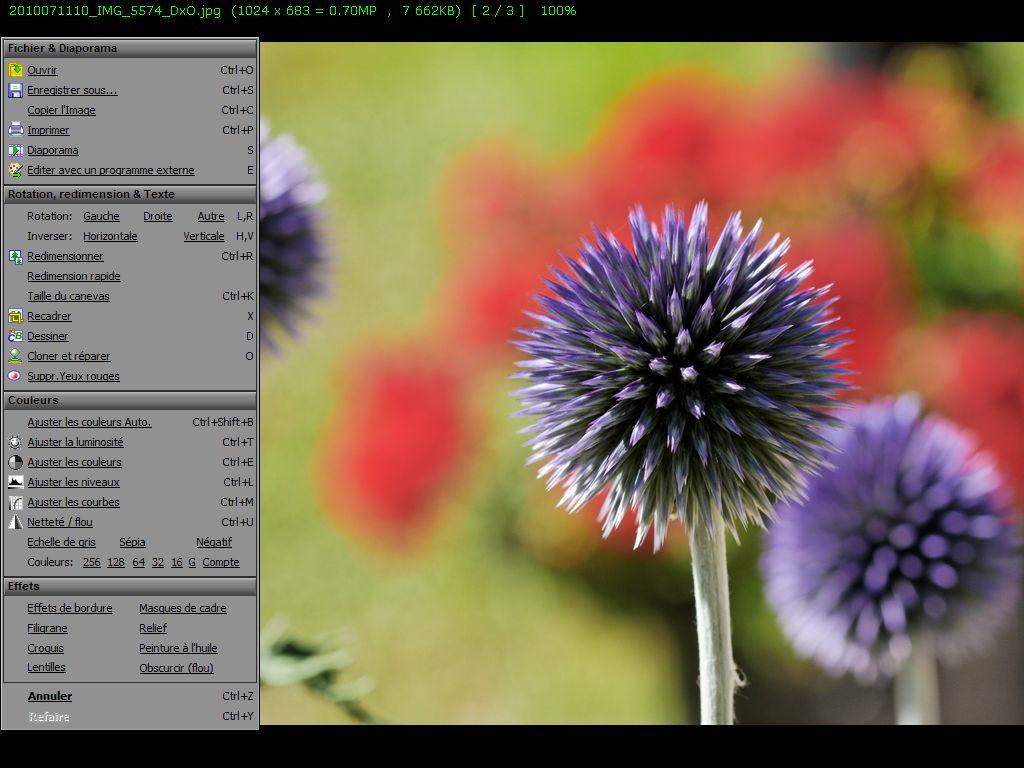
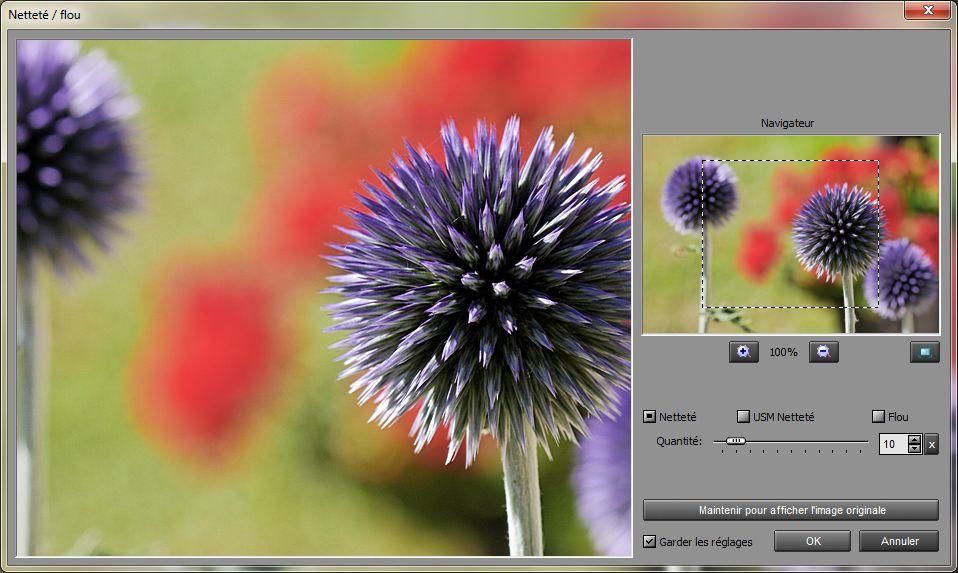
Toujours vérifier que le zoom est à 100%, pour que un pixel de l'image corresponde à un pixel de l'écran. Là, je recommande un réglage à +10, pour une bonne impression visuelle. Tout dépend également de la sévérité de la réduction. C'est là aussi où votre sensibilité à l'accentuation est plus ou moins forte. Attention de ne pas tomber dans l'excès. Faites des essais !
Retour à l'image finalisée. Ouvrons le menu à gauche
Et cliquons sur "Enregistrer sous..."
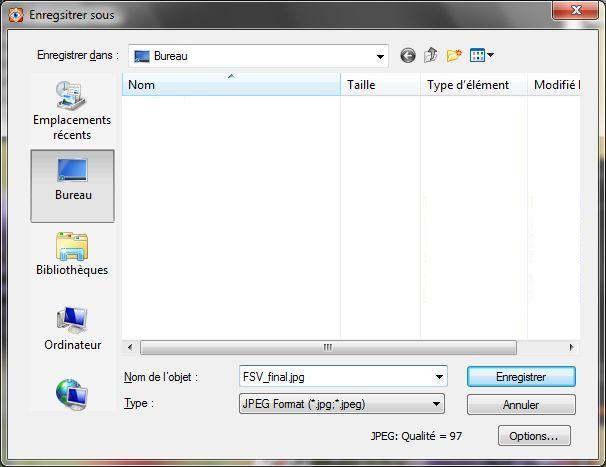
Cliquons sur Options.
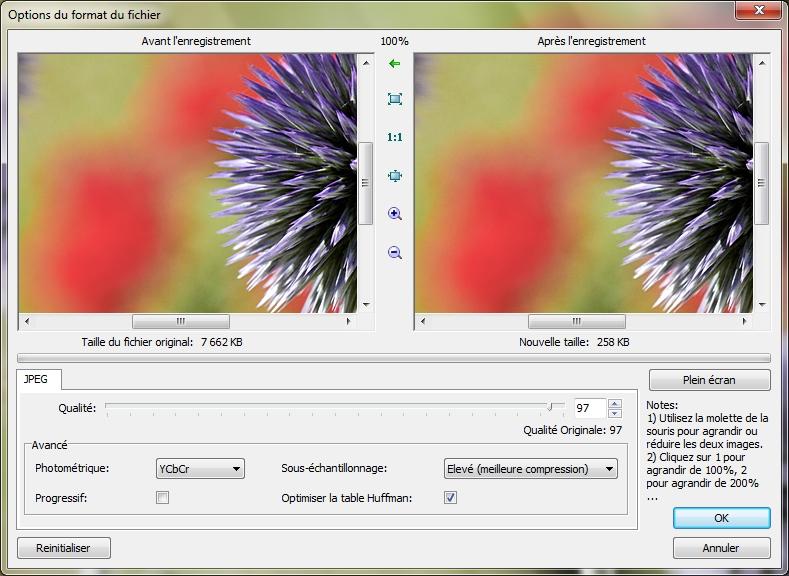
Là, nous allons régler précisément au moyen de la réglette qualité, le taux de compression du JPG. Ainsi, nous pourrons passer juste sous la barre de 300ko, avec la prévisualisation de la taille et de la compression finale, dans la fenêtre. Une fois le bon réglage trouvé (ici 97, 98 fait passer au dessus de 300ko), OK pour quitter la fenêtre d'options, et on enregistre son fichier de manière tout à fait classique.
Au final, notre image a été réduite, elle a été accentuée, sa définition et son poids en ko (je préfère ce terme à "taille" qui peut s'appliquer aussi aux dimensions en px) sont conformes aux normes du forum, sans perte de qualité car sans compression excessive.
Image de départ, affichée à la volée avec FastStone Viewer :

Image traitée pour affichage web :

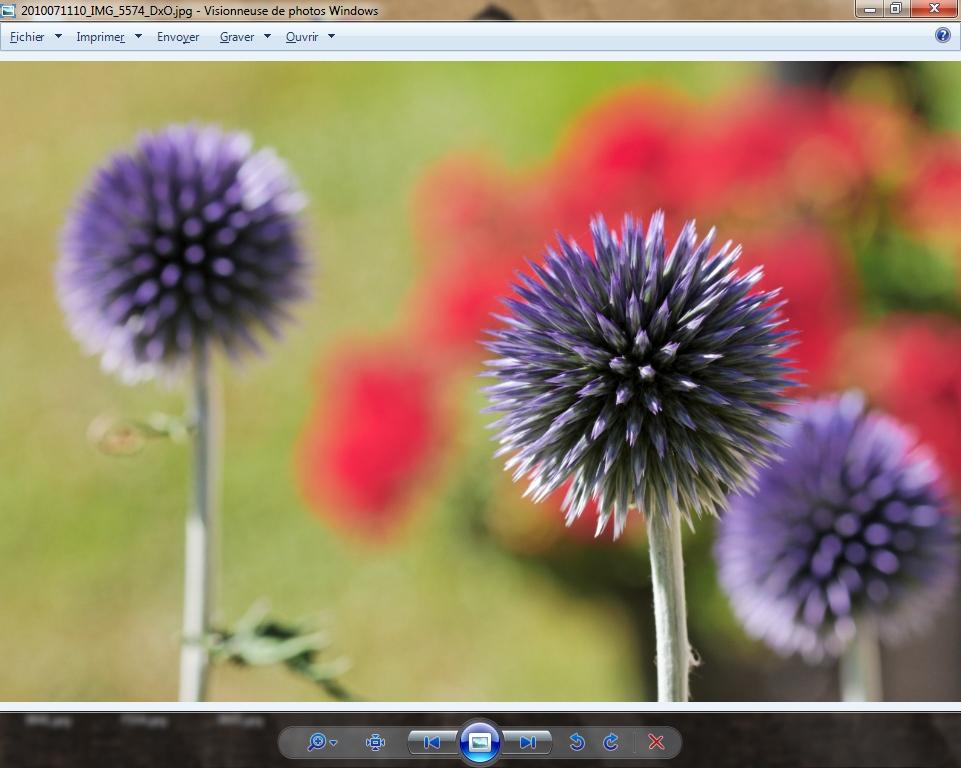
A comparer avec l'affichage de l'original à 18MP dans l'aperçu de Windows. De mon point de vue, il faut vraiment proscrire l'Aperçu pour voir ses images car il induit trop de molesse à l'affichage après redimensionnement à la volée :
Le traitement par lot est aussi possible en allant dans le menu Outils/Convertir les images selectionnées (touche F3)
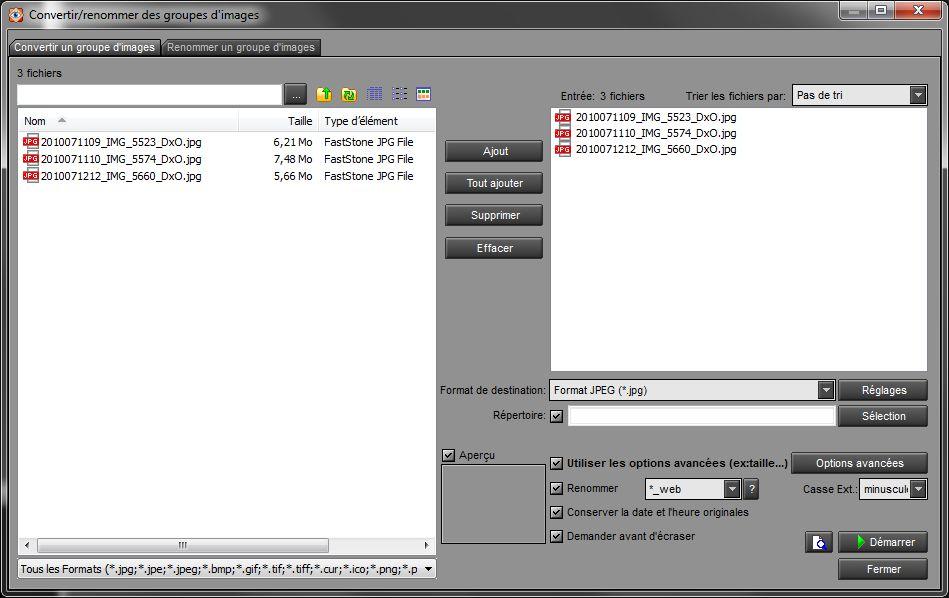
On choisit le répertoire de destination avec le bouton Sélection.
Le bouton Réglages à coté du format de destination permet de régler la compression pour toute la série.
La case Renommer permet de rajouter au bout du fichier un chaine de caractères à votre convenance, comme _web dans cet exemple.
Cliquons sur les options avancées pour choisir le redimensionnement selon la taille choisie et l'accentuation.
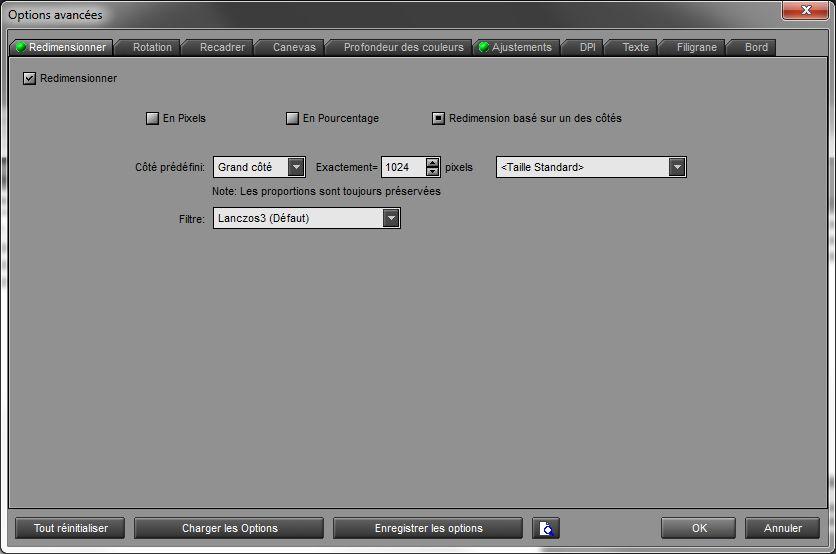
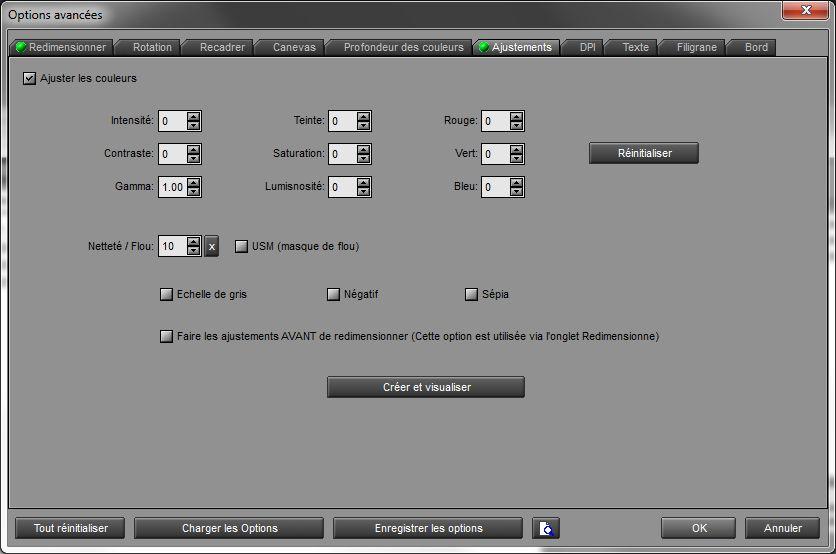
Clic sur OK, puis de retour sur la fenêtre des répertoires source et cible, clic sur Démarrer.
Un bémol toutefois, on ne peut pas créer de profil complets (seuls les réglages des options avancées peuvent être enregistrés et pas le masque de renommage ou la compression JPG). Or nous allons voir avec les profils de BorderMaker que traiter ses images pour l'affichage est utile dans beaucoup de situations et que cela nécessite des paramètres variés.
Avec BorderMaker
Téléchargeable ici : Download | BorderMaker (freeware).
L'intéret de BorderMaker est qu'il permet de traiter tout un répertoire, en lui appliquant le redimensionnement et l'accentuation que vous aurez choisi. C'est aussi possible avec BorderMaker, à ceci près qu'il faut d'abord traiter par lot le redimensionnement, et ensuite traiter par lot l'accentuation pour être sûr qu'elle soit faite après. L'autre intéret, c'est qu'il permet le rajout de cadre, de titre, de texte sur votre photo, si vous le souhaitez (mais ce n'est pas l'objet de ce tuto). C'est le logiciel que j'utilise pour présenter mes images sur EOS-numerique.
Une fois installé, le menu permet une traduction en français, certes incomplète, mais qui peut aider les plus anglophobes d'entre nous.
Voici comment se présente le programme.
Un premier onglet, avec le répertoire source. C'est le répertoire (folder en anglais) de vos images originales.
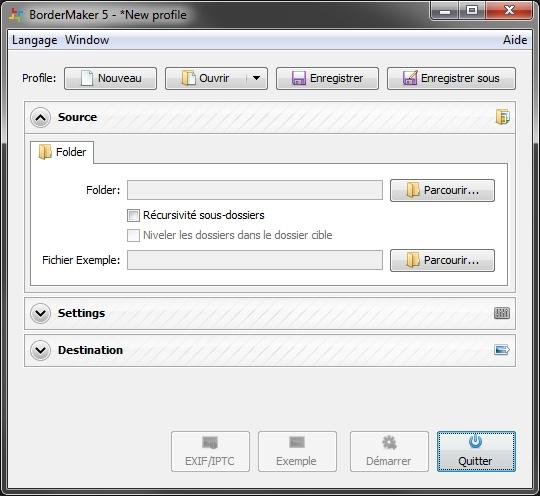
Récursivité des sous-dossier : permet de reproduire l'arborescence des répertoires d'origine dans le repertoire cible. Par exemple, conserver la structure du répertoire "Photos 2011" avec tous ses sous-répertoires, dans le répertoire cible des photos réduites.
Niveler les dossiers dans le dossier cible : permet au contraire de placer toutes les photos réduites dans le répertoire cible, sans création de sous-dossier, quel que soit leur emplacement dans l'arborescence de "Photos 2011".
Un deuxième onglet avec les réglages que je recommande pour EOS-numerique :
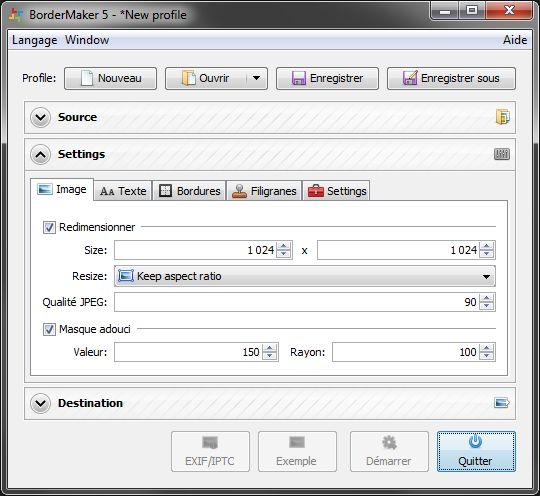
Dans Size, vous remarquerez que j'ai indiqué 1024 à chaque fois. En effet, ce paramètre ne donne pas la taille de l'image finale, mais la dimension maxi souhaitée pour la largeur et la hauteur de l'image. J'indique donc 1024 pour les deux, afin d'avoir des photos horizontales à 1024px de large, et verticales à 1024px de haut.
Keep aspect ratio, soit "conserver les proportions", afin de toujours respecter les proportions de votre image (3:2 avec un reflex Canon EOS).
Concernant la qualité JPEG, on ne peut pas ici optimiser pour chaque image puisque ce profil sera appliqué pour toutes les images du répertoire cible. 90 permet de conserver toutefois une excellente qualité tout en réduisant le poids en ko de l'image. Quand quelques images dépassent la limite autorisée sur EOS-numerique, j'efface les images réduites trop lourdes dans mon dossier cible, je réduis ce paramètre à 85, je relance le processus (qui recommence par défaut pour toutes les images du répertoire source) et à la question (de mémoire) "voulez vous écrasez ce fichier ?", je réponds "non" + "appliquer aux prochains conflits" (procédure classique de Windows quand un fichier risque d'en écraser un autre), afin que seules les images supprimées ne soient retraitées à 85. Les images déjà réduites à 90 ne seront pas écrasées par des versions 85.
Masque adouci : il s'agit du réglage de netteté. Oui, il faut le savoir... Les réglages de BorderMaker sont assez étranges... Je suppose que la valeur correspond à l'intensité, rayon doit correspondre au % d'un pixel (ici, 100% d'un pixel soit un rayon de 1 pixel), et le seuil est absent. Après pas mal d'essai, ce réglage là correspond à ce que je souhaite. Je change parfois la valeur à 180 pour certaines images.
Un sous-onglet très important pour pouvoir maintenir les EXIFs dans les images réduites :
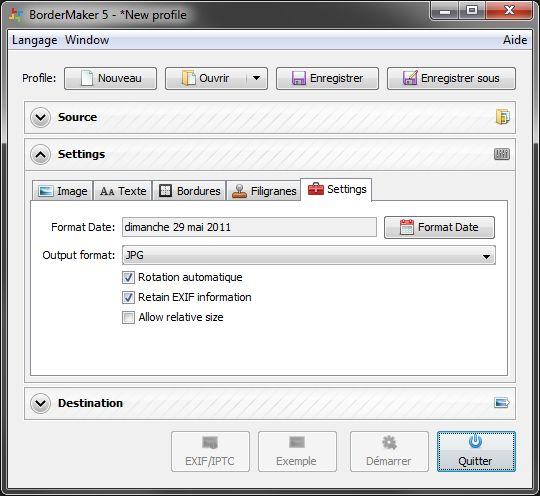
S'assurer que la case Retain EXIF information est cochée. Elle l'est par défaut.
Dernier onglet, celui de la destination avec le sous-onglet fichier :
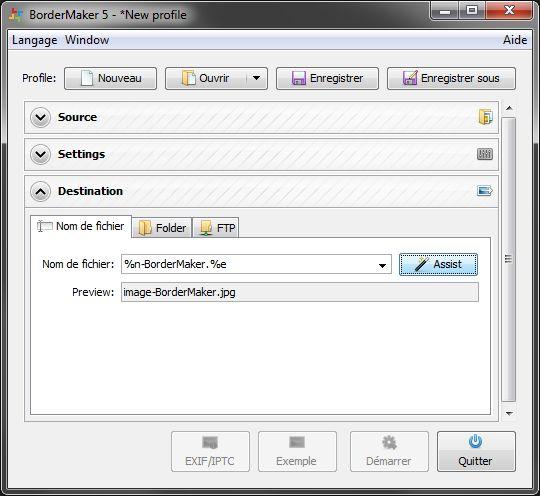
Vous pouvez modifier le nom du fichier. Ici, dans l'exemple, on rajoute -BorderMaker à la fin du nom du fichier. %n, c'est le nom du fichier d'origine. %e, c'est l’extension d'origine. Le bouton Assist vous montre quels jokers vous pouvez utiliser pour renommer automatiquement vos fichiers. Personnellement, je rajoute juste _EOS-num à la fin, pour lire d'un coup d'oeil à quel usage était destinée la réduction.
Le sous-onglet folder permet de renseigner dans quel répertoire vous souhaitez que vos images réduites soient enregistrées :
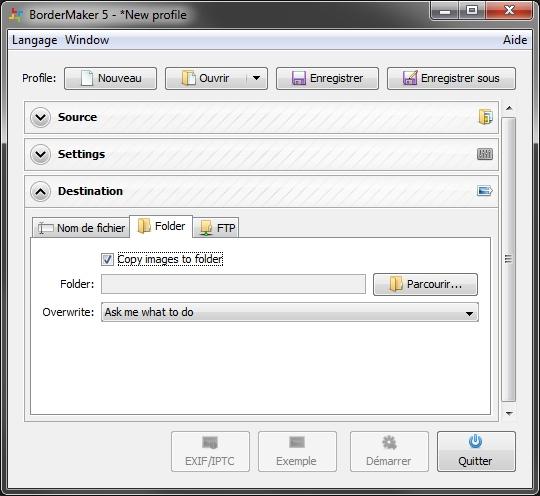
Une fois tout ce paramétrage effectué, vous devez les enregistrer dans un fichier profil, avec le bouton enregistrer sous, toujours présent en haut à droite de la fenêtre. Vous pouvez ainsi créer autant de profils que vous le souhaiter : un pour EOS-numerique, un pour votre site pour lequel vous souhaitez peut être des images plus grandes et moins compressées, un pour un affichage diaporama aux dimensions exactes de votre affichage (lire à ce sujet, la question 13 du tuto "problème d'autofocus ou de netteté"), un pour les envois mail avec des photos plus petites et très compressées, etc...
Une idée : j'ai créé dans mon répertoire "Mes documents" un repertoire "Bordermaker" et un répertoire "BorderMaker réduites", ce qui me permet d'avoir dans tous mes profils et une fois pour toute, un seul repertoire source et un seul repertoire destination. Je copie les photos que je souhaite réduire dans le repertoire destination et je lance mon profil. Ainsi, je ne manipule pas les fichiers originaux, ni les repertoires d'origine, et pas de risque d'écrasement des versions originales par des versions réduites si on a mal configuré la destination et la source (c'est du vécu).
J'espère vous avoir aider ainsi à préparer vos images pour le web en général et pour EOS-numerique en particulier. C'est très facile à faire, avec des logiciels bien conçus, grand public et gratuits, tout en conservant une très grande qualité d'affichage, même avec des JPGs assez compressés, preuve que l'argument consistant à accuser "la compression" pour excuser une image floue ne tient pas. Il faut tout simplement traiter sa photo, pour cet usage particulier.
-
13/02/2012, 14h12 #10Abonné


- Inscription
- avril 2005
- Localisation
- France
- Messages
- 13 986
- Boîtier
- Canon
- Objectif(s)
- Canon EF
 [AIDE] Angle couvert et focale
[AIDE] Angle couvert et focale
Beaucoup de débutants (ou pas d'ailleurs) au moment de compléter ou changer leur objectif se pose la question de l'angle couvert en rapport avec la focale inscrite sur le fut. Les questions sont souvent du type "j'ai un 18-55 ou un 24-105, que m'apportera un 70-200" ou alors "mon objectif actuel ne cadre pas assez serré, quelle focale dois-je prendre pour faire "ça" [avec l'illustration du cadrage souhaité] ?".
En fait, c'est relativement simple, et vous avez trois moyens pour arriver à connaitre tous les cadrages de toutes les focales que vous souhaitez.
1) Sur le web
Les constructeurs offrent sur leur site, un outil visuel qui permet de se rendre compte de l'angle de champ des focales les plus courantes.
Canon propose un outil, pas très dynamique, mais qui fait le job. Les photos sont quand même bien petites. Autre bémol, les angles couverts et les illustrations ne sont valables que pour le 24x36 (mais ce n'est pas précisé).
Canon Focal Length Comparison Photo - Canon France
Sigma propose aussi un outil, plus séduisant visuellement, et qui propose d'emblée le choix de l'optique DC (sur capteur APS-C) ou DG (tout format). A noter qu'on vous demandera avec une optique DG si vous la montez sur un boitier argentique/numerique plein format, ou sur un boitier "numérique" (sic). Pour Sigma, le boitier "numérique" tout-court est donc forcément un boitier APS-C. C'est un abus de langage que nous retrouverons ensuite. Soucis avec cet outil sigma, dans le cas d'un zoom, on a alternativement la photo prise avec le coté court et le coté long du zoom, sans aucune transition, et sans pouvoir figer l'image. Assez perturbant dans la mesure où l'alternance est rapide, ce qui ne facilite pas la comparaison.
http://www.sigma-photo.fr/Medias/Fla...ns%20image.swf
Tamron propose clairement le meilleur outil, avec toutefois la même erreur sémantique qui consiste à considérer le 24x36 comme nécessairement de l'"argentique" et l'APS-C comme du "numérique". Un fois qu'on le sait... Quand vous avez choisi votre format de capteur, donc, vous pouvez choisir votre focale sur la reglette, de manière totalement intuitive et dynamique, en voyant les changement de cadrage en temps réel. Et ce, de 10mm (14mm en 24x36) à 500mm. Vous pouvez aussi limiter la plage de focale à l'objectif qui vous interesse dans la liste à droite, sachant qu'un 70-300 cadre de la même manière chez toutes les marques.
Tamron Europe: Comparaison des longueurs focales
2) A partir d'une photo
Pour connaitre comment cadre, sur son boitier, une focale qu'on ne possède pas, il suffit de prendre une photo de sa collection, prise avec le même boitier et de faire une simple règle de trois. Il faut connaitre la focale de la photo prise, la focale "souhaitée", et les dimensions en pixels de votre photo.
Le rapport des focales est égal au rapport des dimensions des cadres (démonstration que j'avait faite jadis, ici pour ceux qui aiment ça ou qui ont l'esprit de contestation ). Ainsi, un 70-200mm cadrera par rapport aux 55m d'un 18-55, 3,63x plus serré (200 divisé par 55, tout simplement). Il suffit maintenant de diviser la longueur en pixels et la largeur en pixel par 3,63, pour obtenir le cadrage qui vous donnerait un 200mm, si vous l'aviez eu au moment où vous avez pris la photo.
). Ainsi, un 70-200mm cadrera par rapport aux 55m d'un 18-55, 3,63x plus serré (200 divisé par 55, tout simplement). Il suffit maintenant de diviser la longueur en pixels et la largeur en pixel par 3,63, pour obtenir le cadrage qui vous donnerait un 200mm, si vous l'aviez eu au moment où vous avez pris la photo.
Exemple, en vraie dimension pour le forum, à savoir 1024x682 (forum oblige), prise à 18mm avec un 18-55mm (évidemment, c'est à faire chez vous sur votre fichier d'origine, pas la peine de réduire) :

- EXIF: Canon ( EOS 300D DIGITAL) | Canon EF-S 18-55mm F/3.5-.56 | 18mm | 1/100s | f/6.3 | ISO 100
Si je veux savoir ce que j'aurai pu prendre avec un 24-105 à 105mm, je fais 105 divisé ( / ) par 18 = 5,83. Ensuite, 1024/5,83= 175px et 682/5,83 = 117px et ce cadre de 175x117px me donne le cadre depuis mon point de vue, sur ma photo, que j'aurais eu avec 105mm de focale.
N'importe quel logiciel de photo permet de tracer un cadre de 175x117px dans la photo et on obtient :

Ainsi partir d'une focale plus courte, pour cadrer à l'intérieur ce qu'aurait donné une focale plus longue est facile. L'inverse est tout aussi possible, simplement, on ne peut pas à partir d'un cliché à 50mm, "inventer" l'image qu'on aurait eu à 24mm.
On peut tout aussi facilement déterminer à partir d'un recadrage fait sur l'ordinateur de quelle focale on aurait eu besoin. Processus inverse : je veux cadrer serré sur l'église, je fais un cadre en respectant la proportion 3:2 du format d'origine, et dont je mesure ensuite les dimensions en pixels (ici 175x117). Ma photo à 18mm faisait 1024px de large, je divise 1024 par 175, je trouve 5,83. Il me faudra donc une focale 5,83x plus elevée que 18mm soit 105mm.
3) Avec un morceau de carton et un mètre
Merci à geo18 pour cette astuce.
Il suffit de découper dans un carton un rectangle de la taille de son capteur (24mm x 36mm ou 15mm x 22,5mm pour l'APS-C). Il faut ensuite que la distance entre l'oeil et le carton corresponde à la distance focale, pour voir le cadrage correspondant. Donc, carton à 50mm de l'oeil pour voir le cadrage d'un 50mm, 400mm pour un 400mm, etc... La carton tient déjà compte de la taille du capteur, nul besoin d'appliquer un coefficient quelconque.
Informations de la discussion
Utilisateur(s) sur cette discussion
Il y a actuellement 1 utilisateur(s) naviguant sur cette discussion. (0 utilisateur(s) et 1 invité(s))
Discussions similaires
-
Micro-réglages 7d et 24-105
Par estetzein dans le forum Discussions techniquesRéponses: 9Dernier message: 07/05/2012, 16h07 -
Micro réglages sur 5DMKII ou autre.
Par newworld666 dans le forum Discussions techniquesRéponses: 44Dernier message: 11/09/2011, 17h12 -
Micro réglages
Par tipounastre dans le forum Discussions techniquesRéponses: 2Dernier message: 25/03/2010, 13h31 -
Micro-réglages ?
Par Heodrene dans le forum Discussions généralesRéponses: 10Dernier message: 09/03/2010, 20h28 -
Aide lémoire Hyperfocale pour Zenitar ...
Par houba83 dans le forum Trucs et AstucesRéponses: 5Dernier message: 20/04/2006, 20h02